Full Article
Content
- Introduction.
- The Universal Field - deducing and testing.
2.1 Inertia and relative time.
2.1.1 Inertia.
2.1.2 Relative Time.
2.2 Matter, mass and gravitation.
2.3 The puzzling reference frame - the true nature of relativity.
2.4 Matter and antimatter.
2.5 Black holes and supernovas.
2.6 BIG BANG. - The Universal Field Theory vs. existing theories and their consequences.
3.1 Length contraction.
3.1.1 Length contraction part 1.
3.1.2 Length contraction part 2.
3.2 Wave particle duality for all quantum objects.
3.3 Gravitational waves.
3.4 Gravitational time dilation.
3.5 Shapiro time delay. - Proposals for testing the theory with experiments and/or new evaluations of old experiments
- Conclusions
References
Abstract
The Universal Field Theory argues the existence of a field as the medium of existence for everything in the Universe, including light and matter. It demonstrates how this field is the base of a relative, background independent world, and proposes explanations to a number of phenomena present in it, including wave-particle duality, gravity, inertia, black holes, supernovas and Big Bang.
In the process of describing the field we will discover that it can coexist with mathematics of current physics, even though some will be explained differently as a consequence of our findings. Furthermore, the theory will shed new light and logic on some unexplained exceptions and paradoxes of today’s physics.
1. Introduction
The Evolution of Physics (Einstein & Infeld, 1938:95), argues that “to raise new questions, new possibilities, to regard old problems from a new angle, requires creative imagination and marks real advance in science."
This article aims to find new answers to some of the unexplained phenomena and incohesive theories present in current physics. In order to do so we will raise new questions and regard old problems through the most creative lens possible - which I argue to be philosophy. This, while including mathematical demonstrations to test the theories thereof created. When doing so we will return in history and base our reasoning on what has been experimentally proven. For instance, the starting point of our research will be that the speed of light is constant whenever measured locally. However, we will not, by default, accept the further conclusion that the speed of light is independent of the motion of the light source and the frame of reference of the observer, since this never has been proven experimentally.
The universally adopted method in scientific research - the scientific method - consists of making a postulate and to then try and prove it experimentally – or at least suggest experiments that could prove it. In this research we will work by the scientific method, but apply it partly differently to its traditional use. We will, through philosophical reasoning reach a conclusion that we will formulate as a postulate. Thereupon, we will test the postulate philosophically and at the same time explore whether or not it could benefit us in the search for explanations to currently unexplained phenomena and/or paradoxes. Finally, we will further challenge the postulate by completing mathematical tests, as well as propose additional methods to investigate it experimentally. In that process we will establish a strong case for both the probability of its existence and for explanations of unexplained phenomena.
2. The Universal Field - deducing and testing
We begin our reasoning by addressing the properties of light.
Until the beginning of the twentieth century it was widely agreed by the scientific community that light should be moving in a motionless field (d’Inverno 1992, 16). That conclusion was reached by comparing light to sound - which exists as waves propagating through the air. This would deem it logical for light waves to propagate through a medium as well. But since light can move in ‘empty’ space, it was argued that the vacuum must be filled with an invisible carrier - an ether.
On the basis of this conclusion, one further conclusion was drawn, namely that if there is an ether, there should be a so-called ether wind, relating to effects of the Earth moving in the ether. For instance, when the Earth moves in the same direction as the sun through the ether, scientists argued that we should experience a stronger ether wind (Michelson 1881, 120-129). Vice versa, when the Earth moves in the opposite direction, the ether wind should then be weaker.
However, despite accurate measurements in for example the Michelson-Morley experiment (Michelson, and Morley 1887, 333–345), scientists could not detect any ether wind effects, which was considered a severe blow to the theory. As a result, a majority of the scientific community abandoned the idea of an ether, even though some, including Hendrik Lorentz, kept arguing that one still could, and even should, exist. Indeed, Lorentz suggested the so-called Lorentz transformation (d’Inverno 1992, 25-26 and 29-32), which proposed a method allowing to make sense of an ether despite the discoveries of earlier ether wind experiments.
Later, Einstein (Einstein 1916) proposed another solution related to the ether debates. He adhered to the idea that there would not be any motionless ether and instead proposed a theory based on the equation Speed = Distance/Time and the logic that:
Since the speed of light is independent of the motion of the light source (proven experimentally when measured locally), the changeable quantities must be Distance and Time.
Based on this conclusion, and using the so-called Lorentz factor, Einstein had developed formulas on the change of both time (relative time), and distance (length contraction) in his well-known Theory of Relativity, which, in short, stipulates that wherever we are, and however that place travels through space, the laws of physics remain the same. Opposition to this principle only arises when we view a place that does not move in the same speed and direction as ourselves. Furthermore, the differences are identical for two viewers travelling at different speed, viewing each other. This could be interpreted as if each place has its own ether, or in any case not as if there exists one large, motionless ether.
Several of the predictions made by the theory of relativity have been proven to be correct, and the mathematics presented in the theory are coherent with most of modern physics. The theory is thus regarded as fully established in the field. One may then ask oneself how such a theory possibly could be challenged.
There are a number of peculiarities about the theory of relativity. Some have been addressed by Einstein himself in his General Theory of Relativity - such as the fact that time indeed does slow down inside a spacecraft that takes off from another spacecraft - compared to the spacecraft that remains stagnant in space. Yet, it could be argued that some peculiarities are not satisfactorily addressed, and thus remain problematic. One of these is the Ehrenfest paradox (Hrvoje 1999).
The Ehrenfest paradox is, in short, the dilemma that a rotating cylinder of unchanged radius would create different length contractions depending on the rotational speed of the different parts, according to the theory of relativity. This implies that if the outer parts of the cylinder were to rotate at the speed of light they would be of null length - a consequence that is very difficult to both understand and explain.
In order to decompose the theory, one should ask oneself more generally what practical consequences length contraction would bring. If it did indeed exist, and since space would be of different length for all bodies travelling through it at different speeds, space would have all and every size at the same time. This seems unlikely. In fact, length contraction has never been proven experimentally.
So, what would happen with physics if length contraction did not exist then? Would not the theory of relativity, and all its corresponding and proven mathematics, crumble without it?
We will look into that now.
Firstly, let us define light as everything travelling at the speed of light; thus, not only the one visible to our naked eye. We take as a given that the speed of light is constant when measured locally. Let us demonstrate this definition, taking the example of astronauts travelling almost at the speed of light in a spacecraft, from which they shine a light. That light leaves them at the speed of light in all directions. At the same time, regardless of whether the spacecraft travels towards or away from us on the Earth, the same light, when it reaches us, moves at the speed of light compared to us as well. This mean that the light moves marginally faster than the spacecraft when the spacecraft travels towards the Earth, and almost twice the speed of light relative to the spacecraft when the spacecraft departs from the Earth.
Well, if length contraction was ruled out, and considering that we know that time does change with the speed of a system (Botermann, et al. 2014) as seen by an outside observer, the speed of light, as seen by an outside observer, would have to change. We know that the speed of light is constant when measured locally, but we don’t know if it is true that the speed of light is independent of the motion of the light source and the frame of reference of the observer. Indeed, there are some indications that the speed of light could change (as seen by an outside observer) when light travels through space. For instance, the Shapiro time delay test (d’Inverno 1992, 204-205) concluded that the light slowed down as it passed close to the sun (keeping in mind that the additional time taken from a changed path was negligible). With that said, we should attempt a thought experiment of the world without length contraction, to see what that would come to imply.
Let us return to our imagined astronauts traveling at a very high speed in a spacecraft, and shining a light, which, when it reaches us on the Earth, travels at the speed of light also relative to us, independently of the spacecraft’s travel direction.
We know that light always behaves in the same way. Let us therefore assume that it behaves that way out of pure necessity. If this light were to move in total emptiness, it should act like a ball thrown out of a moving car, and travel at a speed being the combination of the emitting substance's speed and the speed of light.
The unavoidable conclusion (in a world where we exclude length contraction), is that light cannot travel in total emptiness. It must exist in, or at least strictly interact with, a medium - a field - in which it, out of necessity, is forced to travel at the speed of light.
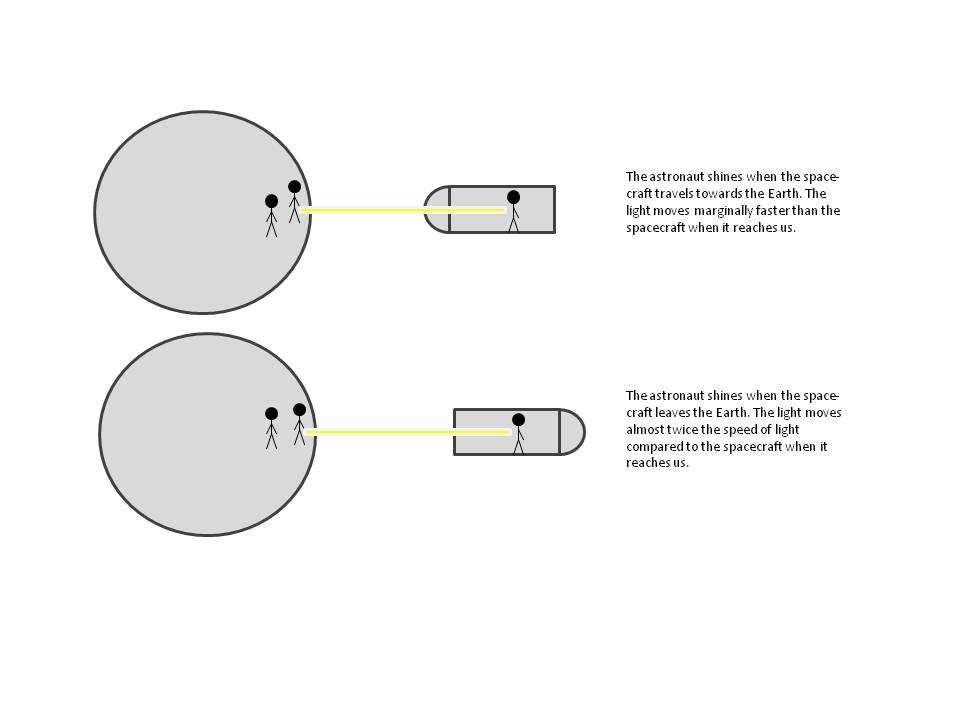
Figure 1. In a world without length contraction the light changes its speed relative to an outside observer
Despite the logic in our reasoning above, it appears such a conclusion lead us to a catch-22 situation, since the ether wind experiments seemed to make it impossible for the existence of a field - a finding which probably also led Einstein to his theory of relativity. But, as we wish to view old problems in new ways, we will go on with our experiment and look into what could be the constitution and properties of a potential field, and whether it could provide us with some clarity. We call this field the Universal Field.
We need to begin with reflecting upon the Universal Field’s very essence.
First of all, we realize that it must be elastic in order to carry light waves. It must also have a certain resistance, since a field without resistance would allow anything to go through it unaffected, making it completely insignificant. Furthermore, it should not be attached at endpoints in a stretched position or contracted by external forces. It should rather be in a resting position, where it stays out of pure necessity, in its lowest energy state. If the energy was to decrease in the field when it was either compressed or extended, it would shrink or extract by itself. It should therefore also resist both compression and extension. Whenever there is movement in the field, with compressions and extensions as a consequence, the field thus must be at a higher energy level compared to its resting position.
If the field was able to carry light faster or slower than the speed of light it most probably would do so, at least at certain points. But since we have no measurements of such behaviour, we have to believe that the speed of light both corresponds to the speed at which the field always transports light, and to the maximum speed it can transport light, which we choose to call the fields maximum adaptation speed.
While these might have been some of the more obvious characteristics of the field, there is more to find under the surface. For example, how would light exist in a seamless field, in a continuum? In such a field, a light wave should behave similarly to a wave on the ocean. When the light wave meets another light wave, or any other form of obstacle, it should simply move through or bounce off it. It is difficult to picture how waves in a continuum would react with each other. It is also difficult to visualize where the outer border of a light ray in a continuum would be, and how a wave could move for years through such a field while largely keeping its energy and form. There are thus reasons to believe that the field is not a continuum, but rather quantified. This means that a single oscillation would exist in a medium which is not fully linked to its surroundings, a medium that could be something resembling a thin thread, attached at its ends in junctions to other, similar, threads. Let us call this thread an arm (see figure 2). Every arm would obviously be extraordinarily small, maybe as small as a Planck length.
Furthermore, there are no indications pointing towards anything but symmetry in the laws of physics. A field should therefore be built in symmetrical patterns, including formations such as, for example, icosahedrons, in all directions.
We thus have a symmetrical, cobweb-like field built by minuscule arms, connected to each other in junctions. These arms must carry light as either a wave, or a compression – both giving practically the same result. Let us, for the sake of simplicity, imagine the light as a wave in an arm.
When a substance emits a light-wave (oscillation) into an arm, the arm must be extended. In order to picture this, let us compare it to the way a rubber band, attached at each end, has to be elongated in order to create a waveform. However, the arm resists the stretch and thus pulls its junctions. The other arms connected to the same junctions and pointing away from the initial arm will then slightly give in and extend. At the same time, the arms positioned in a similar direction as the initial arm will instead be compressed.
Figure 2. Diagram of a field consisting of arms and junctions. The thick arm from which the oscillation is formed, causes a pull at its two junctions, which in turn, extend the dashed arms and compress the double arms.
Let us now try to also picture the oscillation while it moves through the field at the speed of light. It would typically propagate through the original arm, in which it was emitted, until it reaches a junction. From there, arms point in different directions and the oscillation cannot just enter one of them, and leave the other ones unaffected. It will instead make the junction vibrate and, in turn, make the arms attached to it vibrate as well - vibrations that take over some of its energy. These vibrations are probably vital in helping the oscillation proceed into a new arm. The first oscillation will lose some of its energy and become smaller than it was originally, but it is still there, like a small particle. The surrounding vibrations move along with the oscillation as a carrying wave, which follows the oscillation through the field. The oscillation and the carrying wave stick together because of the gravity and the total energy and their direction through the field are preserved - since there is nothing in an unaffected field that can make energy disappear or change direction. This is the configuration of light in its simplest form - a combination of wave-particles propagating through the Universal Field at the speed of light.
We have thereby created a model of the properties and constitution of the field, allowing for light to exist in it. However, we have not yet established why no ether wind would be present in combination with our field.
The idea of an ether wind was based on the belief that the ether existed as a medium only for light, while leaving matter unaffected by it. This is a thought whose logic can be questioned. In fact, how could light possibly be strictly dependent of an ether that leaves matter unaffected, while we know that matter and light simultaneously react with and affect each other? This seems like a highly difficult equation to make sense of. The two properties should not be able to coexist.
We therefore make the assumption that also matter exists in the Universal Field.
But how could matter exist in the field? And what would matter consist of, on a micro-level?
The Universal Field is nothing but the field itself - arms making up a symmetrical cobweb-like net. Matter existing in this field should thus also be made up of oscillations and carrying waves, just like light. But, unlike light, matter can be stagnant in space. The oscillations making up matter should therefore move in circular motion. But, we have just stated that a lonely oscillation (light) has to go straight through an unaffected field. So, for oscillations to move in circular motions they have to bundle into ring-like structures. These rotating rings could, in turn, assemble into different microscopic constellations, resembling, for instance, minuscule gyros, twin-suns or planets rotating around a sun, which could also bundle and build larger and larger constellation until they finally become the particles we know as matter.
If the Universal Field were to consist of patterns in the form of icosahedrons we find that it would be theoretically possible for oscillations to bundle and create stable rotating rings - Figure 3.
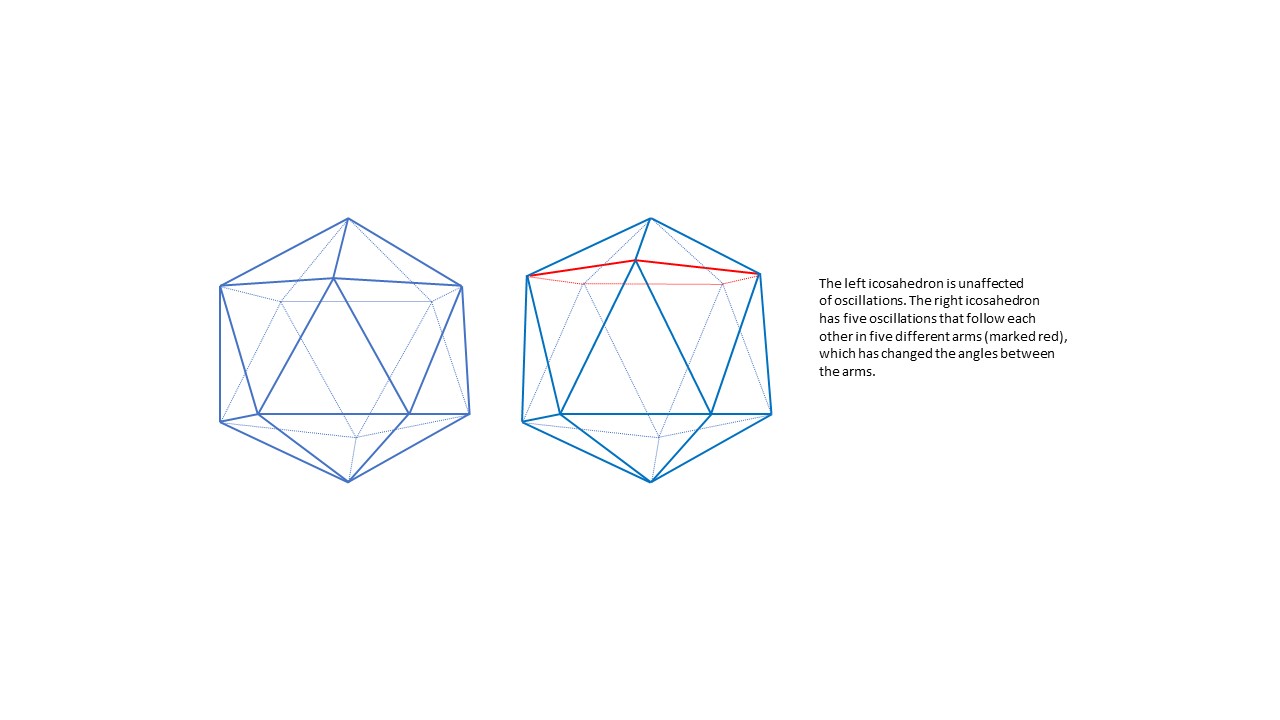
Figure 3. The Universal Field in the shape of icosahedrons, to the left in a resting state and to the right deformed by oscillations. If we examine the icosahedron in the resting state we find that at the end of each arm there are two arms pointing forward that have exactly the same angle out from the arm. If we were to imagine that a mass of particles moved along an arm of that icasohedron and then chose one of the two arms at the end of the arm for their continued journeys, the outcome would be completely random as to which of the two arms the particles would end up in. This because the probabilities would be exactly equal. But if the same particles were to move along one of the red arms of the right icosahedron, the result would be different. In that icosahedron, the angles are changed and it is easier for a particle to continue its journey into a red arm than into any of the other arms and therefore all particles would choose to continue their journey along the red arms. They would thus rotate in a ring. The same applies for oscillations.
This model of the Universal Field brings us to conclude that the one elementary particle, the cornerstone of everything in the universe, is an oscillating arm, and the cornerstone of all matter is a number of rotating oscillations that together create a ring. As a consequence, mass neither has, nor can be transformed into energy according to the formula: E=mc2. Instead, according to the very same formula, mass is energy; a physical quantity of energy, an enormous amount of bundled oscillations.
We have hereby reached the conclusion that there could exist a field, in which both light and matter can exist. However, we have to no extent proven its existence just yet. Rather, we have performed a reasoning in which we have found the likely properties of the field, considering knowledge we have and conclusions we have made throughout. Furthermore, we still have no answer to our original questions - why light always travels at the speed of light when measured locally, and how and why light would change speed as seen by an outside observer. In order to answer these questions, and to further test the probability of the existence of the Universal Field, we will test the theory on some physical phenomenon in the following six chapters. This, with the goal of simultaneously gaining further understanding of these phenomena.
2.1 Inertia and relative time
2.1.1 Inertia
One of the riddles of physics is why mass has inertia. We could also ask ourselves why masses have kinetic energy or constant momentum. These three quantities are undeniably not the same, but it will soon be clear why we despite that fact chose to place them on an equal footing in certain situations.
We have previously found that light must have a carrying wave to propagate through the Universal Field, so what is the case for matter?
Let us picture a number of bundled oscillations, circulating in three ring-like formations around each other, taking the shape of a gyro. Our "gyro" is completely stagnant in the Universal Field - meaning its oscillations rotate, turn after turn, in the same exact arms. Let us imagine that we nudge the gyro for it to move - although such an action is practically impossible of course. It resists the push, but we keep on pushing until it moves, and all its oscillations relocate from one group of arms to another. The oscillations in the gyro cannot proceed to a new group of arms spontaneously, without anything changing. Indeed, the gyro did not move without compulsion. The displacement only occurred when the surrounding arms vibrated to let it happen. These vibrations are energy, which came from the power we used to push the gyro, and they show as a wave movement. Energy is always preserved, so once the wave movement has materialized, it propagates through the Universal Field and continues to carry the gyro, which moves along at a constant speed. We thus have a carrying wave for a minimal particle, just as we had for the light's oscillation.
A carrying wave consists of vibrations, pulling and pushing arms, which make a structure move. Just as for oscillations, it is energy, which, as we have established, is equal to mass. The wave carrying the gyro is thus a mass that we can attribute to the gyro. If we push the gyro harder, it will move faster, which at the same time increases the energy of the carrying wave and consequently the mass that can be attributed to the gyro. Carrying waves thus exist both for the light and for matter propagating through the Universal Field.
The Universal Field is symmetrical in its state of rest. Hence, there is nothing in an unaffected field that could cause a carrying wave to suddenly change. Only could that happen in a field that is influenced by energy. Therefore, the size and direction of a carrying wave is constant over time in an unaffected field.
Based on these conclusions, we derive the following definitions:
Kinetic energy is the amount of energy in the carrying wave of a structure.
The momentum corresponds to the size and direction of the carrying wave of a structure - the higher speed and mass, the larger the size of the carrying wave.
Inertia corresponds to the resistance of the Universal Field to change the momentum, meaning its resistance to change the size and direction of a carrying wave.
Thus, the three quantities are not the same, but all have its origin in the carrying wave of the Universal Field. The answer to what one of them is, will therefore largely be the answer to what the others are.
2.1.2 Relative Time
We will now examine how and why time would move slower in the Universal Field when an object travels faster. We imagine ourselves in a spacecraft that accelerates until it reaches the speed of light. We have concluded that all oscillations always move in the Universal Field's maximum adaptation speed. This must be true both when the spacecraft stands still and when it travels at the speed of light. We therefore realize that when the spacecraft travels at the speed of light, the Universal Field already adapt at its maximum speed to carry the spacecraft. It cannot, simultaneously, adapt to changes of positions of the matter - neither the matter as a whole, nor its inner (rotating) structures - since that would require an ability to adapt more than it already does, while it already adapts at its maximum adaptation speed.
One may ask oneself what this has to do with time?
We can define time as the process of things changing. If we were able to analyse this process, by freezing the world at a particular moment and then unfreezing it for only a microsecond, we would find that during the microsecond, things have happened at both the micro and the macro level. An arm in the field has oscillated, an electron has moved to a new nucleus, a person has just so slightly changed position, and so forth. However, when we freeze the world again, everything stands still. This is just as in our spacecraft, when it travels at the speed of light, because the field is not able to adjust more than it already does. In other words, time stands still. Or expressed differently: when the Universal Field is carrying matter at the speed of light, its remaining maximum adaptation speed is null, meaning no adaptation speed is left in it for moving oscillations in and closely around this matter.
The Universal Field Theory thus coincides with the theory of relativity in terms of relative time due to velocity.
2.2 Matter, mass and gravitation
Let us now use gravity to further test the Universal Field.
At the centre of the Earth, the matter's oscillations and carrying waves push and pull their surrounding arms – just like they do everywhere. This makes the arms compress or extend, resulting in a deformed Universal Field. The impact decreases with distance, but long before it has ceased, other matter will take its turn to push and pull the arms. This continues outwards until the surface of the Earth, where the deformation reaches its climax. One might better understand what the deformed field looks like if we think of it as a fishing-net, being pulled at two opposite ends, making the threads orient themselves with the direction of the pull. The arms whose position is predominantly vertical to the surface of the Earth are being extended, while the arms whose position is predominantly horizontal are being compressed. That is roughly what the field looks like around the Earth; with more arms vertically oriented than in its neutral resting position. Whenever oscillations move in such a field their directional choices will be affected by the asymmetry created, which equals to gravity. Or, in other words, gravity is a phenomenon that arises when the directional choice of moving oscillations is affected by an asymmetrically deformed field.
Since matter can be stagnant in the field, the above reasoning only make sense if all the oscillations making up matter (the smallest ringlike formations) rotate at a very high speed - that logically being at the Universal Field's maximum adaptation speed.
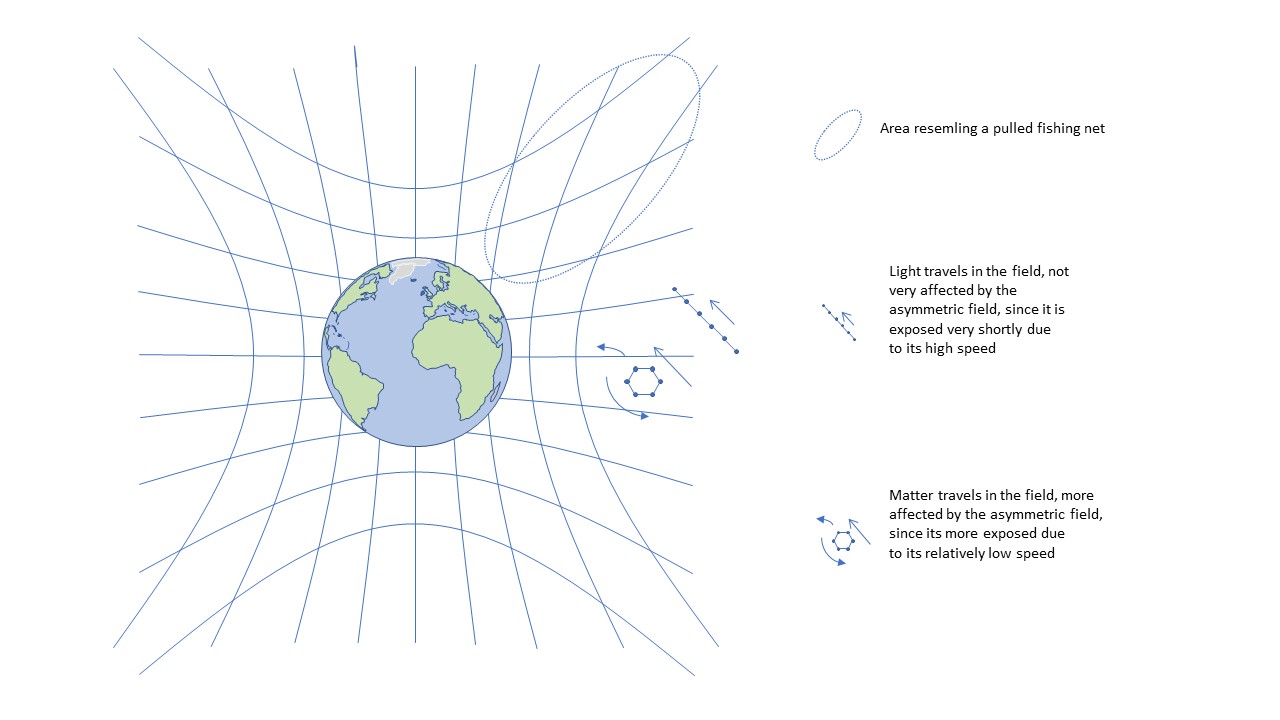
Figure 4. The Universal Field, deformed by the oscillations and carrying waves of the Earth. A small piece of matter, rotating at a very high speed, whose directional choice is being affected by the asymmetrically deformed field to move towards the Earth. Light, is affected as much as matter per time unit, but is propagating so fast through the field that the effect on its direction is considerably smaller than for the matter.
We attempt a definition of gravitational force:
The gravitational force depends on the degree of asymmetry in the Universal Field; in that the greater the asymmetry, the stronger the gravitational force.
It does not matter if the arms are extended or compressed. What matters is whether the field is extended or compressed asymmetrically.
This model of matter and light within the Universal Field seems to work well with what we currently know about gravitation. In fact, it even provides us with a reasonable explanation for the very formation of gravitation.
2.3 The puzzling reference frame - the true nature of relativity
The energy of a carrying wave corresponds to a mass, which can be attributed to the energy it moves. Similarly to gravity, it affects the Universal Field with the greatest impact closest to the carried energy and decreases with distance. Carrying waves are like wind, and when matter is being carried by a wave, it is as if the matter follows the wind, at its very speed. The wind of the carrying waves can be interpreted as a force, affecting the direction of energy, similar to how the wind on the Earth affects, for example, a flying bumble-bee. Just like all matter, the sun has a carrying wave moving it. Around the sun, the wind of the carrying wave "blows" in such a way that everything is affected to follow it. The Earth, being part of the solar system, is under the influence of the sun's carrying wave, together with the rest of the solar system. At the same time, the Earth is moved around the sun by its own carrying wave, which also influences its surroundings. In other words, the carrying waves create their own systems, which seem disconnected from the actual Universal Field, even though they exist within it. Let us study some consequences of this.
Keep in mind that the Universal Field, for all oscillations, adapts in its maximum adaptation speed. But the maximum adaptation speed is available for both carrying waves and oscillations, combined. Thus, when there are carrying waves in the field they absorb a part of the field's adaptability, reducing its further adaptability - as we have seen in chapter 2.1 when we examined relative time. Therefore, the Universal Field's maximum adaptation speed for oscillations - corresponding to the speed of light and time - decreases relative to the strength of the background impact from carrying waves. It may also be relevant to mention that the Universal Field's adaptation speed only is indirectly affected by the rest mass of a structure, by the fact that a larger rest mass requires a larger carrying wave to remain at the same speed.
Furthermore, all oscillations are affected equally by the carrying waves' background impact. As both time and the speed of light are movements of oscillations, they will be affected equally in the same carrying waves. Thus, a measurement of the speed of light will give the same result regardless of the system of carrying waves in which it is made.

Figure 5. The sun and the Earth with their respective carrying waves, whose strengths decrease with distance. If light passes through a carrying wave, its speed will be affected proportionally to the strength of the wave, the same way time is affected. The location of the measurement of the local speed of light will thus not affect the results found. However, if we were able to measure the speed of light inside the solar system from a location outside the same system, we would find differences in the speed of light depending on the position of the light in the carrying waves.
The speed of light relative to a location outside the carrying waves depends on the direction and strength of the "wind" of the carrying waves, and the background impact of the carrying waves, which limits the field's further adaptation speed.
Let us take a space station orbiting around the Earth as an example to analyse the changes in the speed of time. The carrying wave of the Earth is weaker in space than on the surface of the Earth. This means that the background impact of the carrying wave is smaller in space, which results in time going by faster there. At the same time, the space station has its own carrying wave that moves it around the Earth. This extra carrying wave for the space station requires a further adaptation of the Universal Field, which will affect time to go by slower.
With that point made, time is only relevant as a concept when there is energy in the field. Without energy there are no changes in the field, and without change, the concept of time becomes irrelevant.
Furthermore, we cannot travel forward or backward in time; changes in position (which corresponds to time) are final.
It could be useful to introduce the term (local) speed of events, as it could simplify the understanding of both relative (local) time, and the notion that the speed of light is constant. A change in the speed of events is dependent on the background impact of the carrying waves on the Universal Field where the events take place. A changed speed of events results in a change of the speed of all events, including local time and movement of light.
It is relevant to try to understand how the strength of carrying waves vary. We have stated that there are carrying waves for both light and matter. Light is brought forward at the speed of light, meaning that the Universal Field must use its maximum adaptation speed to carry it. Also, we have stated that the Earth is affected by the carrying wave of the sun, which by no doubt travels considerably slower than the speed of light, but obviously affects the Earth much more. So how does the strength of carrying waves change with distance from the carried object?
Let us start by regarding light, which is a single oscillation in a single arm carried forward by a carrying wave. The carrying wave for light should engage all the arms surrounding the central oscillating arm. However, already at the distance of two arms (straight) away, the engagement of the field must be significantly reduced, since many more arms there are being involved in the movement. Indeed, it is reasonable to expect that the carrying wave at this distance will have decreased to a fourth (1/4) of its original strength, corresponding to the change of surface of an imagined sphere at the distance. By the same reasoning, at a distance of four arms, the remaining strength of the wave will only be a sixteenth (1/16). The effect of a light’s carrying wave (if one arm is the size of a Planck length), thus gets to a negligible size after a very small distance - relative to distances in our everyday world. In fact, a carrying wave for light would have as little as a trillionth of its original strength left after the sheer distance of 1,6x10-28 meters from the centre oscillating arm.
While the example with light might be reasonably straightforward, it might be less obvious to understand what happens with the strength of the carrying wave of a larger object. In order to make ourselves a picture of this we will create a simplified model of the pulling of the carrying wave and the way it influences the oscillations making up matter. Firstly, every pull of a structure has to go through the arms - it cannot pass between arms. A carrying wave should logically be of a spherical shape (around a structure), and any pull at one side of the object must have a corresponding pull on the opposite side. In any other case, the pull would create an acceleration. Furthermore, if a pull was to start somewhere in the middle of a structure, it would become a disruptive force. This means that every pull should go through the centre of the structure. Moreover, the force should be applied on the oscillations making up the object, and not beside them. If we would imagine that all oscillations making up the object are being positioned in rows of existing arms from the centre of the object and outwards, the pullings will be equally strong as long as there are oscillations left. Or expressed differently, as far out as the “matter-oscillations” put in rows from the core of the object reaches, the carrying wave is using the same strength to pull - a strength corresponding to the speed of the object. When the “matter-oscillations” are ”finished” (we reach the end of the row of “matter-oscillations”) the force of the pulling will start to be divided between many arms - in a similar way as for the carrying wave of light. The decrease from that point should be in relation to the size of an imagined sphere with a radius equalling the distance created by the “matter-oscillations” put in rows - similarly to the decrease of strength for the carrying wave for light. We call this sphere the carrying wave sphere of an object (see figure 5 below) - a size that will probably correspond to a structure’s Schwarzschild radius, rs=2GM/c2 (where G is a gravitational constant, M is the mass of an object and c is the speed of light), or a quite similar size.
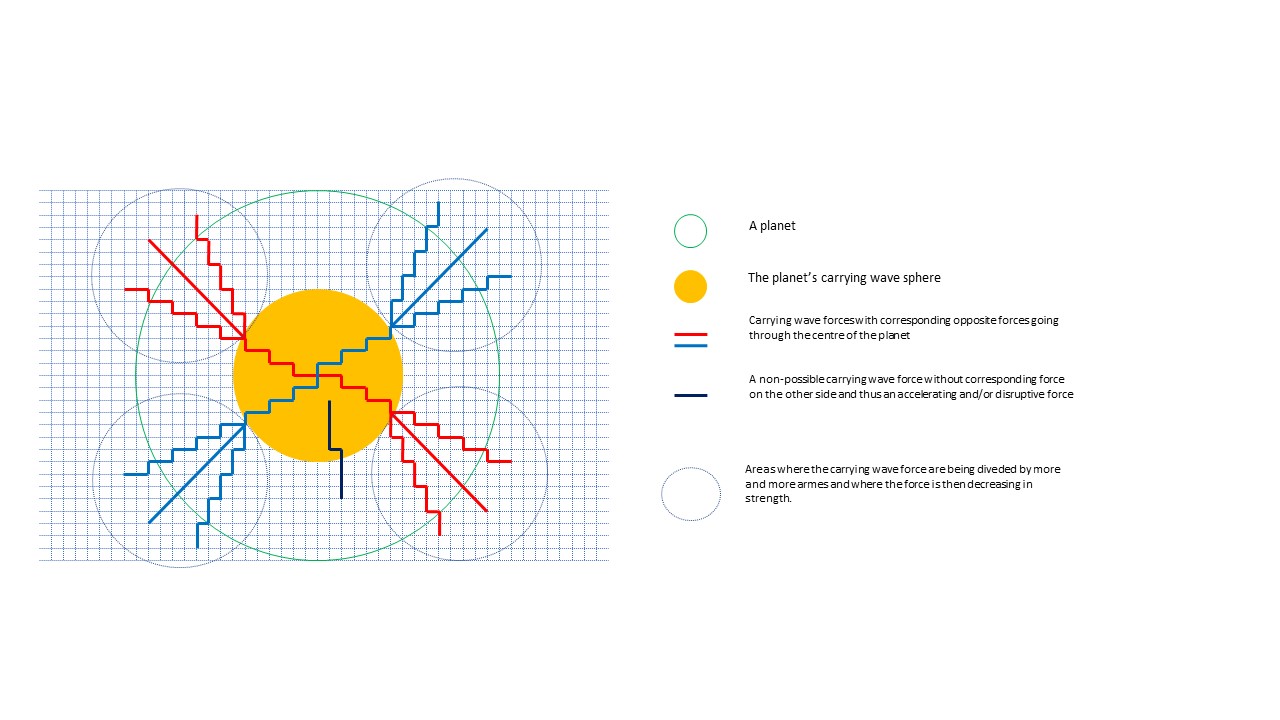
Figure 6. A planet is carried through the Universal Field by a carrying wave that pulls it along existing arms in the field. There cannot exist pulls like the black one displayed, shown to pull the planet without any connection to the centre of the carrying wave, and without a corresponding pull on the opposite side of the planet. The carrying wave sphere of the planet, corresponds to a size where all matter would be collected in the maximum number of existing arms, placed in straight rows outwards from the planet´s centre.
The scientific community normally considers the Schwarzschild radius to define the event horizon - a theoretical limit for the creation of black holes (d’Inverno 1992, 223-225). As discussed above, the Universal Field Theory argues that the Schwarzschild radius could equal the size of a structure when all its rest mass (rest energy) is placed in straight rows of arms from its centre and outwards. If that would be true it could help us to further explain the Universal Field Theory. Indeed, if the smallest microscopic rings of rotating oscillations existed in the smallest possible ring like formations in the field, being smaller than the Schwarzschild radius, it would explain why the oscillations can stay together - as a ring structure - while moving through the field. Furthermore, the reason why these structures would not attract any additional single oscillations would be due to their need to remain smaller than the Schwarzschild radius - in order to stay as stable as possible.
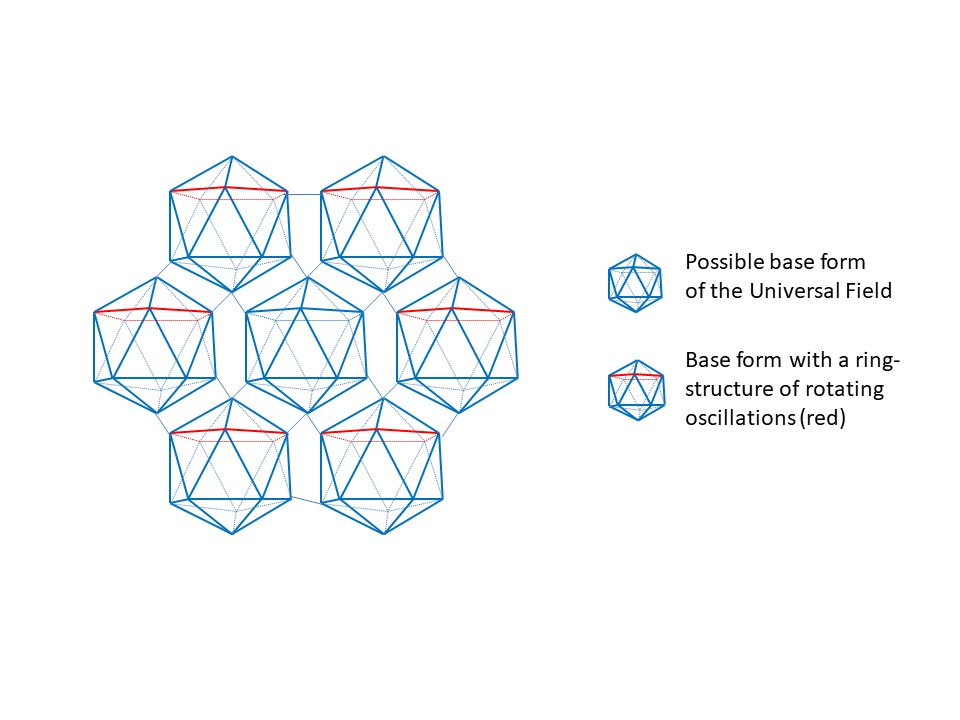
Figure 7. A simplified picture of the Universal Field, consisting of Icosahedrons of arms close to each other, showing how rotating ring structures of oscillations of the smallest possible size would exist in a field.
In this context it should be mentioned that, according to the Universal Field Theory, the so-called gravitational waves affect the Universal Field similarly to carrying waves, by using some of its ability to adapt for movements through the field, and thus affecting the speed of light and time accordingly. But the effects of gravitational waves are normally much smaller than that of carrying waves, meaning they normally can be ignored from the discussion of factors affecting time and the speed of light.
2.4 Matter and antimatter
It is unclear how antimatter is constructed, and why it cannot exist beside matter. But science wrestles more with results from observations showing that the universe seems to be composed of almost only matter (Canetti, et al. 2012) - the so-called baryon asymmetry.
Matter and antimatter are (normally) created in pairs, so it is reasonable to believe that they complement each other. In the Universal Field, matter is built from oscillations and carrying waves, which should also be the case for antimatter. The only way these can complement each other is through the rotational direction of some or all of their inner parts - or the direction of motion through the field, which cannot be of importance for the creation of matter and antimatter. If so, one can draw another interesting conclusion. Considering that corresponding particles and antiparticles are oppositely electrically charged, also this difference should originate from the rotational direction of their inner parts.
The reason why there is more matter than antimatter in universe should originate from one of two reasons - or possibly a combination of both. Either there is a fundamental difference between the probability of the creation of matter and antimatter. Or antimatter is more easily destroyed than matter once it is formed, that is, destroyed without destroying the same amount of matter at the same time. Since scientists have made numerous experiments and concluded that the difference in probability of the creation of antimatter and matter is not big enough to explain the the baryon asymmetry, we choose to focus our efforts on the second potential explanation.
It is not difficult to realize that different types of structures have different chances of surviving in the Universal Field, because they are more or less stable; resistant to outside impact. Matter should thus hold higher chances of surviving in contact with other structures or high energy radiation, while antimatter should be more prone to breaking.
We let our imagination wander freely and picture a structure consisting of a tube-like body and a pair of rings that rotate through the body. The body has a stronger and a weaker side. The rings always rotate in through the weak side of the body of the antimatter and the strong side of the matter. A couple of "gyros" attach to one of the rings on each of the particles and follow them around.
The gyro that reaches the strong side of the body of the particle detaches from the ring and does no damage, while the gyro that reaches the weak side of the body of the antiparticle enters it and breaks it to pieces
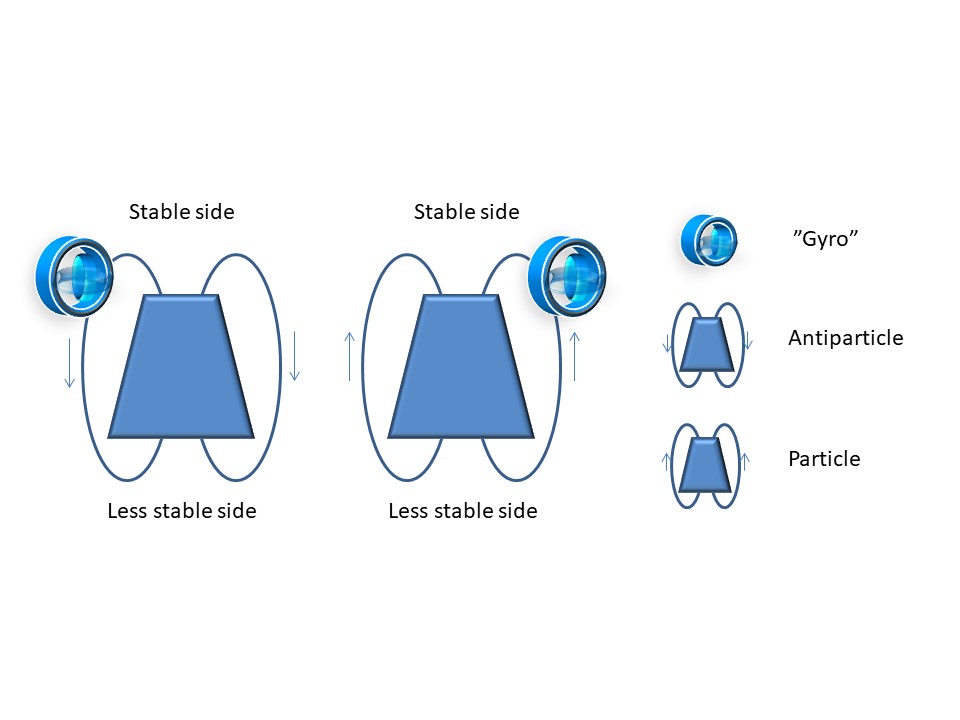
Figure 8. The antiparticle and the particle are build-up of exactly the same components that, however, rotate in different directions. The gyro will come off the ring when it reaches the narrower and more stable side of the tube-like body of the particle, but will enter the wider and less stable side of the tube-like body of the antiparticle and break it apart.
Although this precise model is rather unlikely, given the described components and events, the principle of different stability of particles due to the rotations in their inner parts is the likelier cause of the imbalance between matter and antimatter in universe.
This difference in stability might be difficult to observe on the Earth since the type of intense radiation or microscopic structures that break antimatter (and not matter to the same extent) might be rare here - or at least seldom get in contact with the small amounts of existing antiparticles. So, when and where could the case have been different?
It could certainly have been different in many times and places, but one particularly sticks out as more likely: Big Bang. At Big Bang it is easy to imagine huge amounts of high energy radiations and microscopic structures, which could have slaughtered antimatter to a much higher degree than matter, because of antimatter's weaker structure. This destruction can have continued at a slower pace later on, at other locations.
All this could be true, or not. Either way our reasoning shows that we can find explanations for some of the issues concerning matter and antimatter within the concept of the Universal Field Theory. We have thus, with our reasoning, taken a step in the direction that the Universal Field Theory can be correct, however small it may have been in this chapter.
2.5 Black holes and supernovas
We know that black holes have an enormous density and that gravity around a black hole is so big that no light can escape it. When oscillations in the Universal Field bundle and form matter, they still leave large amounts of arms at rest - meaning arms without oscillations, but still possibly part of carrying waves. The arms at rest are indeed multiple times as many as those that oscillate, even in the middle of matter. So maybe a black hole consists of oscillations that have no, or only minimal, distance between them. Could that work?
We examine this in our imagination by putting together tens of thousands of oscillations into a sphere. On the surface of the sphere there are necessarily many single oscillations, which are not a part of any rotating structures. These will act as any other single oscillations and set off at the speed of light. Eventually, a full micro ring or gyro might leave and not before long the sphere is most likely dissolved. In fact, there is no prerequisite for such a sphere to ever come into existence. There is no way enough oscillations can be collected in a small enough space in order for such a sphere to ever be created - with one exception:
If matter in a big enough celestial body would collapse into single oscillations and enough of these oscillations would collect in a small enough space they could theoretically create a sphere with such a strong gravitation that no oscillations would be able to escape.
Let us further examine this big sphere, consisting solely of dense, non-bundled oscillations. Just as in our previous example with the smaller sphere, oscillations on the big sphere's surface will regularly depart. The difference now would be that enough oscillations are left, staying reasonably tight together, and creating an enough asymmetric Universal Field that makes the escaping oscillations turning around and going back to the sphere before it has had the time to fall apart. Thus, no energy will disappear. We have a stable structure, although its constituent parts are loose oscillations. This corresponds to a so-called black hole.
Let us try to describe one further, through the lens of the Universal Field.
As we have established in a previous chapter, time and the speed of light are affected by the strength of the carrying waves (and not by the total mass of a structure). A black hole has an enormous mass and needs a large carrying wave to move it, so time and the speed of light must be slow in and around it, relative to its surroundings.
Oscillations in a black hole probably often follow each other like currents in an ocean. But sometimes they will not find any way forward, and will then bounce off, like light hitting a mirror. We can therefore imagine two types of black holes; those that mostly rotate and those mostly consisting of bouncing oscillations. However, the rotation of a black hole is a matter of definition. It is impossible for the single oscillations in a black hole to travel around in steady rotations, like matter does on the surface of the Earth. The oscillations' free nature will rather make them act like fish in a shoal, constantly changing places and directions.
The centre of a black hole is without any asymmetry in the Universal Field, and thus without gravity, like the centre of a common planet.
The oscillations are affected by the asymmetrical field and "want" to turn towards the centre of the black hole. The strength of this wish is proportionate to the asymmetry in the field and is thus biggest at the surface of the black hole and zero in its centre.
A black hole must be large enough from the very beginning of its existence in order to collect the evasive oscillations that take off at the speed of light from its surface. This can only be the result of the collapse of a "regular" stable structure with sufficient mass, such as a large star.
A black hole is thus a strange creation. It is extremely dense and produces an extremely asymmetrical Universal Field with resulting extreme gravitation. At the same time, it is a chaotic structure, whose outer parts are in a constant state of dissolution with cascades of oscillations that throw themselves outwards in fruitless attempts to escape, forced back by the inexorable, immensely asymmetrical field. The black hole thus shines with a beaming light, which, yet, is never seen beyond its own world.
Through our description of the black hole we believe to have found the cause of supernovas. A supernova is a star that collapses from a state of stable rotating structures into a structure of single oscillations. Unlike the black hole, however, a supernova is not big enough to have its loose oscillations collecting and, with its own gravitation, retain all the escaping oscillations. The whole structure thus quickly falls apart and we get something that resembles a mini Big Bang - a supernova.
2.6 BIG BANG
A lot indicates that universe came to existence from what is commonly called Big Bang, a kind of original bang that spread out energy and created our planets, solar systems and galaxies (Kolb and Turner 1988). But it is not clear how the bang could have been so exact that the energy spread just right to create universe, instead of either scattering so much that no planets were created, or simply collapsing back into a big lump. And it is hard to understand where all the energy came from, since it seems strange that such a big lump of energy would exist in nothingness and maybe even stranger that it would blow into pieces. Furthermore, there are theories about the existence of parallel universes to ours (Carr 2009), with the obvious consequence that several Big Bangs must have occurred beyond our own.
In the Universal Field Theory, we imagine that the Universal Field exists everywhere in a boundless infinity. For us it is therefore easy and natural to picture an infinite number of universes scattered in this infinity. Such a picture of a mega Universe entails that we would need to see our Big Bang from a broader perspective. It may have been preceded by an infinite amount of other Big Bangs, which could indeed have collapsed back into gigantic lumps or been scattered "by the wind". Our image thus, to some extent, eliminates the question of how Big Bang could have come about at just the right strength.
Let us proceed with the assumption that the law of the conservation of energy is correct. It would mean that all the energy in Big Bang was gathered in a lump just before it began scattering in all directions. Big Bang should thus have been similar to a supernova. However, a supernova arises because a collapsed star is not big enough to keep together when its oscillations becomes free and no longer exist as parts of larger, stable structures. Big Bang must have been many times larger than the largest supernova, and the only type of structure that could contain such amount of energy is probably a giant black hole. But why would a giant black hole blow up like a supernova?
We will examine this question.
It is difficult to imagine that a giant black hole could dissolve from the outside inwards and it seems equally unlikely that it could shatter by a collision. The only reasonable reason why a black hole would explode is due to a force from within.
We know that when smaller suns collapse, they can form supernovas, while only larger suns can form black holes. This makes us believe that maybe only a giant black hole could explode into Big Bang. It seems to us as if something happens with a black hole when it has grown gigantic enough.
All energy in the Universal Field acts the way it does out of pure necessity, because the Universal Field forces it to, so maybe something in the Universal Field forces a black hole to explode when it gets big enough. If that is true, we also make the reflection that all potentially existing universes in the infinite space have very similar amounts of energy.
In the giant black hole's centre, the Universal Field is symmetrically compressed. It being symmetrical does not matter, since it also applies to smaller black holes, but compressed could be the keyword. We have previously stated that oscillations are unaffected by the arms being compressed or not. But while we are convinced that is true for all normal states of the Universal Field, it should be different if the compression is sufficiently extreme. There is probably nothing that does not have an ultimate limit to what it can sustain. So, what would happen to an arm when it no longer sustains more pressure - when it collapses? Perhaps it folds into a small loop or shrinks into a thick and rigid arm. Whatever it does, the result should correspond to a fuse, which suddenly decreases its length and pressure, with the further result that it can no longer carry any oscillations.
The first arm to collapse should be one in the very centre of the giant black hole, where the pressure, theoretically, is the biggest. Let us assume that it folds into a small loop. What happens then? The surrounding field will first crash in over it and then come to a sudden stop, when the arm's two junctions meet, which will increase the pressure on the surrounding arms that were already at the limit of their ability. They will then collapse as well, one after the other in an outward direction from the centre of the black hole, whereupon the oscillations are forced to move in the same direction. The oscillations leave the centre of the giant black hole in a Universal Field that no longer follows its normal laws, as it no longer has its normal properties.
Note that such a process contains quite some violence. The whole resembles the demolishment of a high building by blowing up its bottom floor. When the bottom floor disappears and the rest of the building lands on the firm ground, the force of the fall will help to demolish the following floors.
Most likely, all arms would return from their "fuse blowing state" to a normal one when all the oscillations have disappeared far away and there is no longer any pressure on them. But they could return to normal earlier than that. Once they do, probably two things happen. Firstly, the necessity for the oscillations to leave the centre of the (former) black hole ceases, which increases the likelihood of the black hole being recreated. But in addition, the arms regain more normal lengths, leading to an inflationary expansion of the size of the black hole, meaning that the oscillations suddenly find themselves much further out from the (former) black hole's centre, where their joint impact on the field is smaller and the asymmetry and gravitation they create thus becomes smaller as well. When the oscillations in that situation are sufficiently scattered, they will not reassemble, but instead spread in a Big Bang.
Observe that the inflationary expansion can be many times faster than the speed of light. The speed of light equals the Universal Field's maximum adaptation speed for transporting energy. But the time for a single arm to regain its normal length is without doubt extremely small and many arms can regain their lengths at the same time. If all arms would regain their lengths simultaneously the time for the inflationary expansion of the Universal Field could be similar to the time it takes for the light to propagate through a single arm.
3. The Universal Field Theory vs. existing theories and their consequences
3.1 Length contraction
3.1.1 Length contraction part 1
Length contraction has been supposedly proven mathematically in a few different ways. Below we present one.
We imagine that John stands on the Earth, and observes Emma who departs in a spaceship towards another planet located exactly one light year away from the Earth. Emma travels at the speed v=c-570 m/s, and experiences the equivalent of one minute passing, while a year passes for John.
Let L0 be the length that John experiences and L the length that Emma experiences between the Earth and the planet. ΔT0 is the time Emma experiences between her departure from the Earth and the time she arrives and ΔT the time John experience for the same happening.
We get: v=L0/ΔT=L/ΔT0, which in turn means that: L0/L=ΔT/ΔT0
A commonly made conclusion from this result is that, since relative time has been proven experimentally, we have proven the existence of length contraction.
The reasoning above is based on the postulate that the speed of light is constant in all systems for all observers, independently of the reference frame. Such a position may once have been necessary to explain relativity without the existence of a field. However, this postulate can, and should, now be challenged given the Universal Field Theory´s explanation of how relativity and a field can co-exist.
Indeed, the Universal Field has some elasticity, meaning it can be extended and compressed, but these changes are marginal. And any extension at one place will result in a contraction at another place - and vice versa. If we would view distances between galaxies or even sun-systems or planets these changes would therefore be negligible.
What changes, according to the Universal Field Theory, is thus not the length. In every instance, the lengths and distances are absolute in the field. Instead it is the speed of light that changes - as seen by an outside observer.
In order to understand and explain such a view we need to introduce a zero-point, as a basic reference frame, where the field is unaffected by any energy - in principle a place outside our universe, even though the larger part of our universe is probably more or less unaffected.
From such a zero-point one can fully understand and measure movements in the field, carrying waves and their effects on the speed of light and time.
Instead of length contraction we have a constant length and we get:
L=v*ΔT0=v0*ΔT, and thus: v/v0=ΔT/ΔT0,
where v0 is the speed John experiences Emma to travel in, conforming to the example above, and v the speed Emma experience she travels in. Emma thus experiences that she travels at a speed considerably faster than the speed of light - indeed about 525 000 times the speed of light.
Let us see how Luke, standing at a zero-point would view the speed of Emma, and the speed of light close to Emma. First of all, he would experience that the light Emma shines from the spacecraft would leave her at the speed of c0=570 meters per second (since all events close to Emma - time as well as the speed of light - passes at the speed of only one part out of about 525 000 compared to the zero-point). He would consider that Emma has the speed of c-570 meters per second through the field. The light she shines forward would thus travel at the speed c, also compared to him (c-570+570), and the light she shines backward will travel at the speed of c-2*570 meters per second forward - in the same direction as Emma. Emma’s speed in relation to Luke and compared to the speed of light close to her (c0) would be about 525 000 ((c-570)/c0).
Emma´s speed through the field can thus never be faster than the speed of light when using a zero-point as reference, and it can only be established with exact preciseness by an observer outside all carrying waves (or someone who knows the exact effect of carrying waves of its local place). Nevertheless, it can be calculated with large accuracy by someone in weak carrying waves. We also conclude that the notion of speed can vary depending of the used reference frame.
3.1.2 Length contraction part 2
In a discussion about length contraction, it seems crucial to ask what its processes would be – if it did after all exist.
Matter is built up by small particles rotating around each other at very large relative distances. Why would space be affected by such a matter propagating through it at high or low speed? Why would even all the distance between these minuscule pieces of matter disappear when matter travels through it at the speed of light - making the rotations change into a two-dimensional world? More generally we should ask ourselves how space could have different extension everywhere depending of the speed of matter at one place, and how it could be that the same space would have an infinite number of extensions simultaneously (since it would indeed be of different size for all different matter propagating through it at different speed).
Any advocate of the length contraction should consider these types of questions.
Finally, it should be said, that for example the Ehrenfest paradox never come into consideration when discussing the ins and outs of in the Universal Field Theory, since there is no length contraction according in the theory, and since all extensions and compressions in the field are affecting space and matter equally in all dimensions.
3.2 Wave particle duality for all quantum objects
In the Universal Field Theory all objects are carried through the field by a carrying wave. This is in line with findings in quantum mechanics stating that all objects have a wave-particle duality (Greiner 2000). When combining the Universal Field Theory with these findings we attain both a mathematical and a logical explanation to this phenomenon.
3.3 Gravitational waves
In the Universal Field Theory, both matter and light exist in the field as oscillations moving through arms. When the arms are compressed or extended due to the effects of oscillations, carrying waves or gravitational waves all local changes in length will be equal for both light and matter. It is therefore impossible to detect any change in length of one using the other, by measuring stretches.
This could seem contradictory to the findings about the change of length of matter, which were performed when light was used as a measurement method to prove gravitational waves (Abbot et al. 2106). One could thereof argue that the change of length has been experimentally proven. But the Universal Field Theory wishes to differ.
There is indeed a change in the length of matter due to gravitational waves – if we use a zero point as reference. When the gravitational waves pass a measurement equipment they will, to a small extent, change the size of matter, in such a way that arms are compressed and/or extended, but this change will, as just stated above, also appear for light, which - like matter - exist in the arms. So, according to the Universal Field Theory, the experiment using light to measure changes in distance when gravitational waves passed did not prove that change. Instead it proved that the field’s further ability to carry energy decreased due to the background impact of the passing gravitational waves, which lowered the speed of light.
3.4 Gravitational time dilation
Both the theory of relativity and the Universal Field Theory conclude that time (that is, according to the Universal Field Theory, all changes of positions of oscillations in the field, including the movement of light) runs slower close to a massive structure than it does further away from it (Einstein 1916). But the theories differ in their explanations as to why. The theory of relativity states that the speed of time is affected by gravitation. On another hand the Universal Field Theory claims that the speed of time differs because of the carrying wave of the structure. For both explanations, the outcome remains similar; since a carrying wave is stronger the closer it gets to the structure it carries, just as for gravitation.
According to the Universal Field Theory, the strength of a carrying wave, and thus time (as described in chapter 2.3), depends on r and the Schwarzschild radius (rs) - just like the mathematics in the theory of relativity. The difference between the theory of relativity and the Universal Field Theory is thus not mathematical, even though the Universal Field Theory does not consider the present mathematic to necessarily be true, but still correct as relative formulas. Instead, the differences exist in the understanding of why and how the time dilation due to distance from an object occur.
3.5 Shapiro time delay
The Shapiro time delay test concludes that the light indeed slowed down when it passed close to the sun (d’Inverno 1992, 204-205). The contribution to the extra time from a changed path was negligible. This test was then used to supposedly prove gravitational time delay. But while it certainly proves that the light has changed its speed, it contradicts the postulate of the theory of relativity that the speed of light is always constant (independently of the speed of the light source and the reference frame of the observer), but goes in line with the claim of the Universal Field Theory, stating that the speed of light slows down when the light travels through a stronger carrying wave (which is the case closer to the sun).
4. Proposals for testing the theory with experiments and/or new evaluations of old experiments
There are a number of similarities between the Universal Field Theory and earlier theories, including the relative world and the slowing down of time close to a celestial body. But we also reach a number of different conclusions, which we could test with the help of previous experiments and/or new methods of evaluation.
Arguably, one of the biggest practical change comes from our idea that light indeed changes its speed relative to a zero point when passing through carrying waves, which surround celestial bodies. There are two ways to measure this phenomenon. The first one is to measure that the speed of light can slow down at all, which is more or less done in the Shapiro time delay test. But experiments can also take into consideration the “wind” of the carrying waves. This could, for example, be done by sending an object into space at a very high speed, from which we would shine a light backwards. We could then measure that the light is brought with the object forwards, by the object’s carrying wave. There should also be differences in the speed of light for light passing close to big celestial bodies depending of whether it travels with or against the carrying waves. This difference should also appear when light passes through galaxies. It should take longer for light to reach a certain point after passing through a galaxy that distances itself from the Earth - when the light travels towards the Earth - than it takes when it passes through a galaxy that approaches the Earth. If light was to pass through many galaxies that travel against its own travel direction, the delay could become so significant that its redshift would be affected. Indeed, when we consider the redshift of light, we should take into consideration that the light, according to the Universal Field Theory, slows down when entering all carrying waves, of, not only large constellations like galaxies, but also their smaller parts, sun systems and planets. Even if it might not be considered as a direct proof of the Universal Field Theory, analyses of the slowing down of light and its corresponding redshift, from all possible carrying waves, which would lead to the conclusion that our universe does not increase its speed of expansion, could be seen as an indication that the theory is correct.
5. Conclusions
The Universal Field Theory argues, and reaches the conclusion, that there exists a field as the base of everything in universe, including light and matter. The field consists of threadlike arms connected in junctions, most likely creating symmetrical patterns. Matter exists as oscillations creating rings that bundle into larger structures. Light exists as oscillations travelling in linear motion through the field. Both matter and light are carried through the field by carrying waves. Thus, both matter and light have a wave-particle duality. Furthermore, all oscillations always travel through the arms at the field´s maximum adaptation speed, corresponding to the speed of light. Oscillations making up matter are rotating at this very high speed.
Furthermore, the theory argues that a field must be elastic and resist both compression and extension. Space can therefore be considered bent whenever it is affected by energy, which pulls or pushes the arms.
In the process of evaluating the credibility of the field, we analysed a number of physical phenomena and tested them against the theory, reaching conclusions about what they could be:
One being that the asymmetrically deformed field is causing gravitation, since such a field affects the oscillations directional choices.
A second one being that a field’s inertia is easily understood as the field´s resistance to changes of the speed and direction of a given energy movement.
The theory also finds explanations for why and how the world is relative. It reaches the conclusion that the field´s maximum adaptation speed equals the limit speed at which the arms can carry energy. This limited ability is being used up simultaneously by both the oscillations and the carrying waves. A carrying wave thus has an effect on the field´s oscillations in the way that a stronger carrying wave will use more of the field´s ability to adapt, resulting in its oscillations not being able to move as fast as it would in a field that is less affected by carrying waves. At the same time, a carrying wave is like a wind in the field, affecting all oscillations existing in it to move along with it. The speed of light corresponds to time, and both these quantities depend on how much the field is affected by carrying waves. The speed of light is always related to the strength of the carrying waves, and is therefore constant in relation to the wind of the carrying wave - and not to the stagnant field.
The Universal Field Theory also explains the difference between matter and antimatter as being differences in rotational directions, something which, in turn, is likely to also affect the electrical charge of a particle.
Finally, the Universal Field Theory reaches a couple conclusions about large structures. It finds explanations for the creation of black holes, being a consequence of large number of free oscillations coming close together and creating a strong enough gravitational force to make even escaping oscillations turn around and return. The creation of the black hole is normally a result of a large object made up of matter falling into pieces and becoming free oscillations - light. If the free oscillations do not create a black hole they could instead create a supernova.
A black hole that becomes sufficiently big will create such a pressure on the arms in the field that the arms collapse, making the field lose its normal properties. Eventually, the collapsed arms will regain their normal shape, causing the field to experience an inflationary expansion, being the outset of a Big Bang.
All these conclusions are reached through a philosophical reasoning based on experimentally proven phenomena, such as relative time and the constant speed of light when measured locally. Simultaneously, non-proven theories making non-intuitive or paradoxical conclusions are either left untreated and/or replaced by new solutions.
While a variety of phenomena are being treated and given possible explanations by the Universal Field Theory, it would never claim to have either addressed or resolved all questions out there. It therefore urges anyone to both challenge and test the theory further in order to proceed with the quest to understanding the world.
References
- Abbot, B.P, Abbot, R, Abbot, T.D, Abernathy, M.R, Acernese, F, Ackley, K., Adams, C, et al. 2016. Observation of Gravitational Waves from a Binary Black Hole Merger. https://arxiv.org/ftp/arxiv/papers/1602/1602.03837.pdf
- Ashby, Neil. 2003, “Relativity in the Global Positioning System”, Living Reviews in Relativity 6: 15-18. Available at: https://link.springer.com/content/pdf/10.12942%2Flrr-2003-1.pdf
- Boterman, B, Bing, D, Geppert, C, Gwinner, G, Hänsch, T, Huber, G, Karpuk, S, et al. 2014, Phys. Rev. Lett 113, 120405.
- Canetti, L., Drewes, M. and Shaposhnikov, M. 2012, New J. Phys 14. 095012, arXiv: 1204.4186.
- Carr, B. 2009. Universe or Multiuniverse? UK: Cambridge University Press.
- Nicolic Hrvoje. 1999, Relativistic contraction and related effects in noninertisal frames. Available at:
- https://arxiv.org/pdf/gr-qc/9904078.pdfEinstein, Albert. 1916 Relativity: The Special and General Theory. Translated by Robert W. Lawson, Methuen & Co Ltd. Available at:
- http://www.gutenberg.org/files/5001/5001-h/5001-h.htmEinstein, A. and Infeld, L. 1938. The Evolution of Physics. 1st ed. London: Cambridge University Press. Available at: https://archive.arg/details/evolutionofphysi033254mbp.
- Greiner, W. 2000. Quantum Mechanics, An Introduction. Germany: Springer-Verlag Berlin Heidelberg New York.
- d’Inverno, Ray. 1992. Introducing Einstein’s relativity. Oxford: Clarendon Press.
- Kolb, E and Turner, M. 1988. The Early Universe Perseus Books.
- Michelson, A. 1881. “On the Relative Motion of the Earth and the Luminiferous Ether”. American Journal of Science 3, no 22: 120-129.
- Michelson, A. and Morley, E. 1887. “On the Relative Motion of the Earth and the Luminiferous Ether”. American Journal of Science 3, no 34: 333–345.
This site is owned and managed by Enma Förlag
© Copyright Enma Förlag